AVL Tree

AVL Tree

 AVL adalah balanced binary search tree dimana ia memiliki perbedaan jumlah node pada subtree kiri dan subtree kanannya maksimal 1 (atau dapat dikatakan antara tingginya sama atau selisih satu).

Contoh Gambar AVL Tree

AVL Tree | Set 1 (Insertion) - GeeksforGeeks

Node AVL Tree, karena  balance factor tertingginya 2, sedangkan syarat AVL adalah selisihnya maksimal 1
Cara menentukan Height dan Balance Factor :Note :
Height :
– Jika node (root) tidak memiliki subtree heightnya = 0
– Jika node adalah leaf, height =  1
– Jika internal node, maka height =  height tertinggi dari anak + 1
Balance Factor :
-selisih height antara anak kiri dan kanan, jika tidak memiliki anak, dianggap 0.
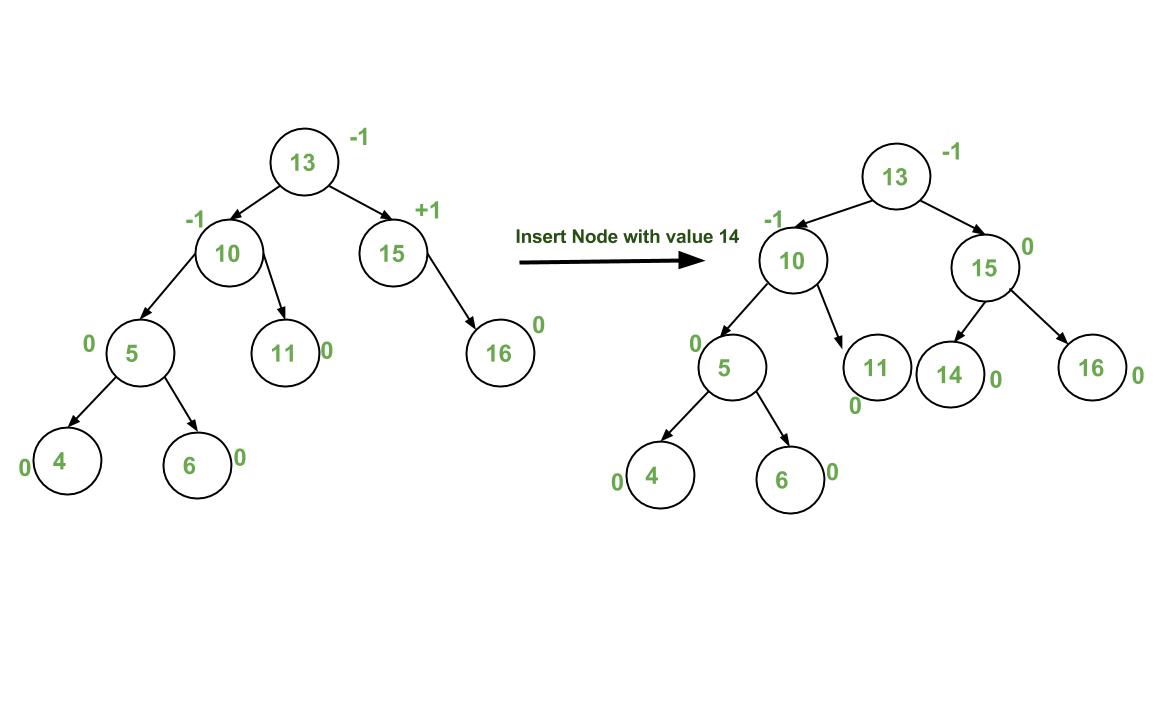
Penambahan node di AVL Tree
     Untuk menjaga tree tetap imbang, setelah penyisipan sebuah node, dilakukan pemeriksaan dari node baru → root. Node pertama yang memiliki |balance factor| > 1 diseimbangkan. Proses penyeimbangan dilakukan dengan: Single rotation dan Double rotation

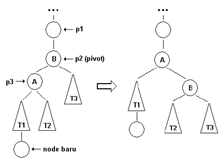
Single Rotation

Single rotation dilakukan bila kondisi AVL tree waktu akan ditambahkan node baru dan posisi node baru seperti pada gambar 2. T1, T2, dan T3 adalah subtree yang urutannya harus seperti demikian serta height- nya harus sama (≥ 0). Hal ini juga berlaku untuk AVL tree yang merupakan citra cermin (mirror image) .


Double Rotation

Double rotation dilakukan bila kondisi AVL tree waktu akan ditambahkan node baru dan posisi node baru seperti pada gambar 3. T1, T2, T3, dan T4 adalah subtree yang urutannya harus seperti demikian. Tinggi subtree T1 harus sama dengan T4 (≥ 0), tinggi subtree T2 harus sama dengan T3 (≥ 0). Node yang ditambahkan akan menjadi child dari subtree T2 atau T3. Hal ini juga berlaku untuk AVL tree yang merupakan citra cermin (mirror image) 



AVL Tree Operations : Deletion

Operasi penghapusan node sama seperti pada Binary Search Tree, yaitu node yang dihapus digantikan oleh node terbesar pada subtree kiri atau node terkecil pada subtree kanan. Jika yang dihapus adalah leaf, maka langsung hapus saja. Namun jika node yang dihapus memiliki child maka childnya yang menggantikannya. Namun setelah operasi penghapusan dilakukan, cek kembali apakah tree sudah seimbang atau belum, jika belum maka harus diseimbangkan kembali. Cara menyeimbangkannya pun sama seperti insertion.












Comments

Post a Comment

Popular posts from this blog

Hash Table & Binary Tree

Image
Hash Table & Binary Tree Hash Table Hash Table adalah struktur data yang mempunyai tabel dan fungsi yang berguna untuk  memetakan nilai kunci yang unik untuk setiap record (baris) menjadi angka (hash) lokasi record tersebut dalam sebuah tabel. Berikut adalah contohnya yang saya ambil dari geeksforgeeks; Operasi Pada Hash Tabel : Insert: diberikan sebuah key dan nilai, insert nilai dalam tabel Find: diberikan sebuah key, temukan nilai yang berhubungan dengan key Remove: diberikan sebuah key,temukan nilai yang berhubungan dengan key, kemudian hapus nilai tersebut GetIterator: mengambalikan iterator,yang memeriksa nilai satu demi satu Berikut kode yang saya dapatkan dari tutorialspoint.com :  #include <stdio.h> #include <string.h> #include <stdlib.h> #include <stdbool.h> #define SIZE 20 struct DataItem {    int data;       int key; }; struct DataItem* hashArray[SIZE];  struct DataItem* dummyItem; s
Read more

Binary Search Tree

Image
Binary Search Tree Apa itu Binary Serach Tree ? Binary Search Tree  adalah  struktur data yang mengadopsi konsep Binary Tree namun terdapat aturan bahwa setiap clild node sebelah kiri selalu lebih kecil nilainya dari pada  root node . Ada beberapa cara dalam menggunakan search tree : Setiap child node sebelah kiri harus lebih kecil nilainya daripada root nodenya. Setiap child node sebelah kanan harus lebih besar nilainya daripada root nodenya. Berikut saya lampirkan gambarnya : Berikut saya lampirkan contoh codingan yang saya ambil dari mahircoding.com : #include <stdio.h> #include <stdlib.h> //inisialisasi struct struct data{ int number; //pointer untuk menampung percabangan kiri dan kanan data *left, *right; }*root; //fungsi push untuk menambah data void push(data **current, int number){ //jika pointer current kosong maka akan membuat blok data baru if((*current)==NULL){ (*current) = (struct data *)malloc(sizeof data); //mengisi data
Read more